11. Exercices

Note

Les exercices sont de difficulté variable, de ★ (simple) à ★★★ (complexe).

11.1. Introduction

11.1.1. Intégration: méthode des rectangles ★

La méthode des rectangles permet d’approximer numériquement l’intégrale d’une fonction f:

\[\int_a^b f(x)\,\mathrm{d}x \approx h \sum_{i=0}^{n-1} f(x_{i}) \quad\text{avec}\quad h = (b-a)/n \quad\text{et}\quad x_i = a + (i+1/2)h.\]

On définit la fonction sq renvoyant le carré d’un nombre par (cf. Fonctions):

def sq(x) :
    return x**2

Écrire un programme calculant l’intégrale de cette fonction entre a=0 et b=1, en utilisant une subdivision en n=100 pas dans un premier temps. Quelle est la précision de la méthode, et comment dépend-elle du nombre de pas?

11.1.2. Fizz Buzz ★

Écrire un programme jouant au Fizz Buzz jusqu’à 99:

1 2 Fizz! 4 Buzz! Fizz! 7 8 Fizz! Buzz! 11 Fizz! 13 14 Fizz Buzz! 16...

11.1.3. PGCD: algorithme d’Euclide ★★

Écrire un programme calculant le PGCD de deux nombres (p.ex. 756 et 306) par l”algorithme d’Euclide.

11.1.4. Tables de multiplication ★

Écrire un programme affichant les tables de multiplication:

1 x 1 = 1
1 x 2 = 2
...
9 x 9 = 81

11.2. Manipulation de listes

11.2.1. Crible d’Ératosthène ★

Implémenter le crible d’Ératosthène pour afficher les nombres premiers compris entre 1 et un entier fixe, p.ex.:

Liste des entiers premiers <= 41
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41]

11.2.2. Carré magique ★★

Un carré magique d’ordre n est un tableau carré n × n dans lequel on écrit une et une seule fois les nombres entiers de 1 à n², de sorte que la somme des n nombres de chaque ligne, colonne ou diagonale principale soit constante. P.ex. le carré magique d’ordre 5, où toutes les sommes sont égales à 65:

11	18	25	2	9
10	12	19	21	3
4	6	13	20	22
23	5	7	14	16
17	24	1	8	15

Pour les carrés magiques d’ordre impair, on dispose de l’algorithme suivant – (i,j) désignant la case de la ligne i, colonne j du carré; on se place en outre dans une indexation « naturelle » commençant à 1:

1. la case (n,(n+1)/2) contient 1 ;

2. si la case (i,j) contient la valeur k, alors on place la valeur k+1 dans la case (i+1,j+1) si cette case est vide, ou dans la case (i-1,j) sinon. On respecte la règle selon laquelle un indice supérieur à n est ramené à 1.

Programmer cet algorithme pour pouvoir construire un carré magique d’ordre impair quelconque.

11.3. Programmation

11.3.1. Suite de Syracuse (fonction) ★

Écrire une fonction suite_syracuse(n) retournant la (partie non-triviale de la) suite de Syracuse pour un entier n. Écrire une fonction temps_syracuse(n, altitude=False) retournant le temps de vol (éventuellement en altitude) correspondant à l’entier n. Tester ces fonctions sur n=15:

>>> suite_syracuse(15)
[15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]
>>> temps_syracuse(15)
17
>>> temps_syracuse(15, altitude=True)
10

11.3.2. Flocon de Koch (programmation récursive) ★★★

En utilisant les commandes left, right et forward de la bibliothèque graphique standard turtle dans une fonction récursive, générer à l’écran un flocon de Koch d’ordre arbitraire.

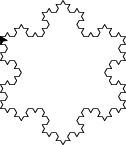
Fig. 11.1 Figure: Flocon de Koch d’ordre 3.

11.3.3. Jeu du plus ou moins (exceptions) ★

Écrire un jeu de « plus ou moins »:

Vous devez deviner un nombre entre 1 et 100.
Votre proposition: 27
C'est plus.
[...]
Vous avez trouvé en 6 coups!

La solution sera générée aléatoirement par la fonction random.randint(). Le programme devra être robuste aux entrées invalides (« toto », 120, etc.), et aux lâches abandons par interruption (KeyboardInterrupt).

11.3.4. Animaux (POO/TDD) ★

Téléchargez le fichier animaux.py et exécutez les tests prédéfinis (dans la seconde partie du fichier) via la ligne de commande (à éxecuter dans un terminal système):

$ py.test animaux.py

Dans un premier temps, les tests échouent, puisque le proto-code (dans la première partie du fichier) n’est pas encore correct. L’exercice consiste donc à modifier progressivement les classes Animal et Chien pour qu’elles passent avec succès tous les tests. C’est le principe du Test Driven Development (voir Développement piloté par les tests).

11.3.5. Jeu de la vie (POO) ★★

On se propose de programmer l’automate cellulaire le plus célèbre, le Jeu de la vie.

Pour cela, vous créerez une classe Life qui contiendra la grille du jeu ainsi que les méthodes qui permettront son évolution. Vous initialiserez la grille aléatoirement à l’aide de la fonction random.choice(), et vous afficherez l’évolution de l’automate dans la sortie standard du terminal, p.ex.:

...#..#.....##.......
.....###.............
#........#...........
.....#...#...........
................##...
.....#.#......##..#..
..............##.##..
..............##.##..
................#....

Astuce

Pour que l’affichage soit agréable à l’oeil, vous marquerez des pauses entre l’affichage de chaque itération grâce à la fonction time.sleep().

11.4. Manipulation de tableaux (arrays)

11.4.1. Inversion de matrice ★

Créer un tableau carré réel \(\mathsf{r}\) aléatoire (numpy.random.randn()), calculer la matrice hermitienne \(\mathsf{m} = \mathsf{r} \cdot \mathsf{r}^T\) (numpy.dot()), l’inverser (numpy.linalg.inv()), et vérifier que \(\mathsf{m} \cdot \mathsf{m}^{-1} = \mathsf{m}^{-1} \cdot \mathsf{m} = \mathsf{1}\) (numpy.eye()) à la précision numérique près (numpy.allclose()).

11.4.2. Median Absolute Deviation ★

En statistique, le Median Absolute Deviation (MAD) est un estimateur robuste de la dispersion d’un échantillon 1D: MAD = median(| x - median(x) |).

À l’aide des fonctions numpy.median() et numpy.abs(), écrire une fonction mad(x, axis=None) calculant le MAD d’un tableau, éventuellement le long d’un ou plusieurs de ses axes.

11.4.3. Distribution du pull ★★★

Le pull est une quantité statistique permettant d’évaluer la conformité des erreurs par rapport à une distribution de valeurs (typiquement les résidus d’un ajustement). Pour un échantillon \(\mathbf{x} = [x_i]\) et les erreurs associées \(\mathrm{d}\mathbf{x} = [\sigma_i]\), le pull est défini par:

• moyenne optimale (pondérée par la variance): \(E = (\sum_{i} x_i/\sigma_i^2)/(\sum_i 1/\sigma_i^2)\);

• erreur sur la moyenne pondérée: \(\sigma_E^2 = 1/\sum(1/\sigma_i^2)\);

• définition du pull: \(p_i = (x_i - E_i)/(\sigma_{E_i}^2 + \sigma_i^2)^{1/2}\), où \(E_i\) et \(\sigma_{E_i}\) sont calculées sans le point i.

Si les erreurs \(\sigma_i\) sont correctes, la distribution du pull est centrée sur 0 avec une déviation standard de 1.

Écrire une fonction pull(x, dx) calculant le pull de tableaux 1D.

11.5. Méthodes numériques

11.5.1. Quadrature et zéro d’une fonction ★

À l’aide des algorithmes disponibles dans scipy:

• calculer numériquement l’intégrale \(\int_0^\infty \frac{x^3}{e^x-1}\mathrm{d}x = \pi^4/15\);

• résoudre numériquement l’équation \(x\,e^x = 5(e^x - 1)\).

11.5.2. Schéma de Romberg ★★

Écrire une fonction integ_romberg(f, a, b, epsilon=1e-6) permettant de calculer l’intégrale numérique de la fonction f entre les bornes a et b avec une précision epsilon selon la méthode de Romberg.

Tester sur des solutions analytiques et en comparant à scipy.integrate.romberg().

11.5.3. Méthode de Runge-Kutta ★★

Développer un algorithme permettant d’intégrer numériquement une équation différentielle du 1er ordre en utilisant la méthode de Runge-Kutta d’ordre quatre.

Tester sur des solutions analytiques et en comparant à scipy.integrate.odeint().

11.6. Visualisation (matplotlib)

11.6.1. Quartet d’Anscombe ★

Après chargement des données, calculer et afficher les propriétés statistiques des quatres jeux de données du Quartet d'Anscombe:

• moyenne et variance des x et des y (numpy.mean() et numpy.var());

• corrélation entre les x et les y (scipy.stats.pearsonr());

• équation de la droite de régression linéaire y = ax + b (scipy.stats.linregress()).

Tableau 11.1 Quartet d’Anscombe

I		II		III		IV
x	y	x	y	x	y	x	y
10.0	8.04	10.0	9.14	10.0	7.46	8.0	6.58
8.0	6.95	8.0	8.14	8.0	6.77	8.0	5.76
13.0	7.58	13.0	8.74	13.0	12.74	8.0	7.71
9.0	8.81	9.0	8.77	9.0	7.11	8.0	8.84
11.0	8.33	11.0	9.26	11.0	7.81	8.0	8.47
14.0	9.96	14.0	8.10	14.0	8.84	8.0	7.04
6.0	7.24	6.0	6.13	6.0	6.08	8.0	5.25
4.0	4.26	4.0	3.10	4.0	5.39	19.0	12.50
12.0	10.84	12.0	9.13	12.0	8.15	8.0	5.56
7.0	4.82	7.0	7.26	7.0	6.42	8.0	7.91
5.0	5.68	5.0	4.74	5.0	5.73	8.0	6.89

Pour chacun des jeux de données, tracer y en fonction de x, ainsi que la droite de régression linéaire.

11.6.2. Diagramme de bifurcation: la suite logistique ★★

Écrivez une fonction qui calcule la valeur d’équilibre de la suite logistique pour un \(x_0\) (nécessairement compris entre 0 et 1) et un paramètre \(r\) (parfois noté \(\mu\)) donné.

Générez l’ensemble de ces points d’équilibre pour des valeurs de \(r\) comprises entre 0 et 4:

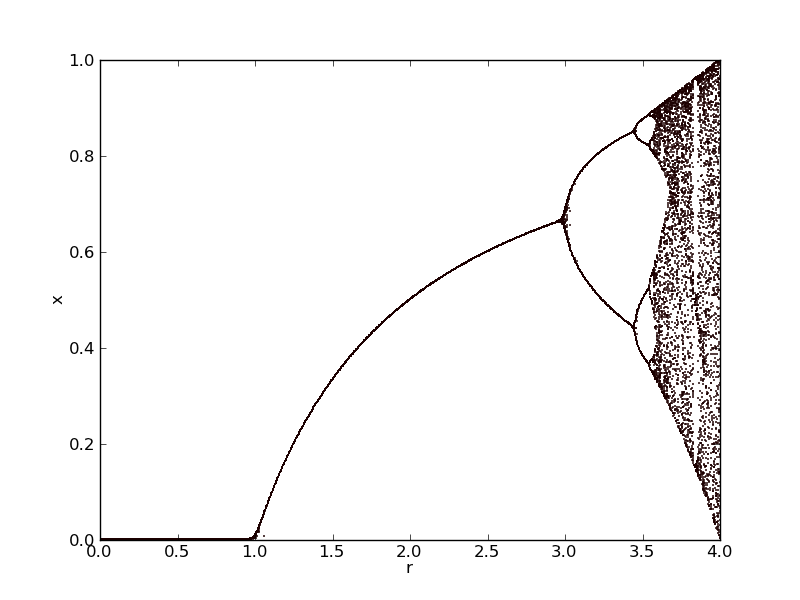
Fig. 11.2 Figure: Diagramme de bifurcation.

N.B. Vous utiliserez la bibliothèque Matplotlib pour tracer vos résultats.

11.6.3. Ensemble de Julia ★★

Représentez l”ensemble de Julia pour la constante complexe \(c = 0.284 + 0.0122j\):

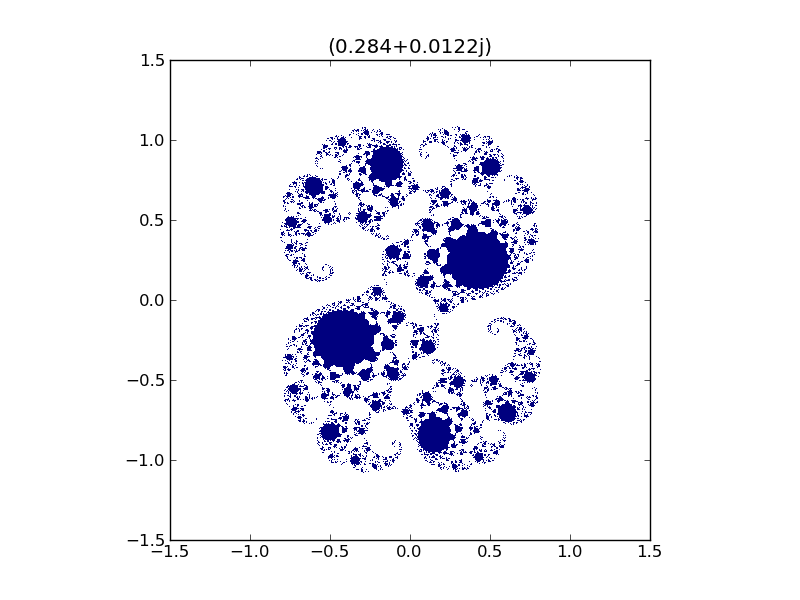
Fig. 11.3 Figure: Ensemble de Julia pour \(c = 0.284 + 0.0122j\).

On utilisera la fonction numpy.meshgrid() pour construire le plan complexe, et l’on affichera le résultat grâce à la fonction matplotlib.pyplot.imshow().

Voir également: Superposition d’ensembles de Julia

11.7. Mise en oeuvre de l’ensemble des connaissances acquises

11.7.1. Équation différentielle ★

À l’aide de la fonction scipy.integrate.odeint(), intégrer les équations du mouvement d’un boulet de canon soumis à des forces de frottement « turbulentes » (en \(v^2\)):

\[\ddot{\mathbf{r}} = \mathbf{g} - \frac{\alpha}{m}v\times\mathbf{v}.\]

Utiliser les valeurs numériques pour un boulet de canon de 36 livres:

g = 9.81       # Pesanteur [m/s2]
cx = 0.45      # Coefficient de frottement d'une sphère
rhoAir = 1.2   # Masse volumique de l'air [kg/m3]
rad = 0.1748/2 # Rayon du boulet [m]
rho = 6.23e3   # Masse volumique du boulet [kg/m3]
mass = 4./3.*N.pi*rad**3 * rho           # Masse du boulet [kg]
alpha = 0.5*cx*rhoAir*N.pi*rad**2 / mass # Coeff. de frottement / masse
v0 = 450.      # Vitesse initiale [m/s]
alt = 45.      # Inclinaison du canon [deg]

Voir également: Équations de prédation de Lotka-Volterra

11.7.2. Équation d’état de l’eau à partir de la dynamique moléculaire ★★★

Afin de modéliser les planètes de type Jupiter, Saturne, ou même des exo-planètes très massives (dites « super-Jupiters »), la connaissance de l’équation d’état des composants est nécessaire. Ces équations d’état doivent être valables jusqu’à plusieurs centaines de méga-bar ; autrement dit, celles-ci ne sont en aucun cas accessibles expérimentalement. On peut cependant obtenir une équation d’état numériquement à partir d’une dynamique moléculaire.

Le principe est le suivant : on place dans une boite un certain nombre de particules régies par les équations microscopiques (Newton par exemple, ou même par des équations prenant en considération la mécanique quantique) puis on laisse celles-ci évoluer dans la boite ; on calcule à chaque pas de temps l’énergie interne à partir des intéractions électrostatiques et la pression à partir du tenseur des contraintes. On obtient en sortie l’évolution du système pour une densité fixée (par le choix de taille de la boite) et une température fixée (par un algorithme de thermostat que nous ne détaillerons pas ici).

On se propose d’analyser quelques fichiers de sortie de tels calculs pour l’équation d’état de l’eau à très haute pression. Les fichiers de sortie sont disponibles ici; leur nom indique les conditions thermodynamiques correspondant au fichier, p.ex. 6000K_30gcc.out pour \(T = 6000\) K et \(\rho = 30\) gcc. Le but est, pour chaque condition température-densité, d’extraire l’évolution de l’énergie et de la pression au cours du temps, puis d’en extraire la valeur moyenne ainsi que les fluctuations. Il arrive souvent que l’état initial choisi pour le système ne corresponde pas à son état d’équilibre, et qu’il faille donc « jeter » les quelques pas de temps en début de simulation qui correspondent à cette relaxation du système. Pour savoir combien de temps prend cette relaxation, il sera utile de tracer l’évolution au cours du temps de la pression et l’énergie pour quelques simulations. Une fois l’équation d’état \(P(\rho,T)\) et \(E(\rho,T)\) extraite, on pourra tracer le réseau d’isothermes.

Indication

Vous écrirez une classe Simulation qui permet de charger un fichier de dynamique moléculaire, puis de tracer l’évolution de a température et de la densité, et enfin d’en extraire la valeur moyenne et les fluctuations. À partir de cette classe, vous construirez les tableaux contenant l’équation d’état.

11.8. Exercices en vrac

• Exercices de base

• Entraînez-vous !

• Learn Python The Hard Way

• Google Code Jam

• CheckIO

11.8.1. Points matériels et ions (POO/TDD)

Pour une simulation d’un problème physique, on peut construire des classes qui connaissent elles-mêmes leurs propriétés physiques et leurs lois d’évolution.

La structure des classes est proposée dans ce squelette. Vous devrez compléter les définitions des classes Vector, Particle et Ion afin qu’elles passent toutes les tests lancés automatiquement par le programme principal main. À l’exécution, la sortie du terminal doit être:

***************** Test functions *****************
Testing Vector class... ok
Testing Particle class... ok
Testing Ion class... ok
******************** Test end ********************

************* Physical computations **************
** Gravitationnal computation of central-force motion for a Particle with mass 1.00, position (1.00,0.00,0.00) and speed (0.00,1.00,0.00)
=> Final system : Particle with mass 1.00, position (-1.00,-0.00,0.00) and speed (0.00,-1.00,0.00)
** Electrostatic computation of central-force motion for a Ion with mass 1.00, charge 4, position (0.00,0.00,1.00) and speed (0.00,0.00,-1.00)
=> Final system : Ion with mass 1.00, charge 4, position (0.00,0.00,7.69) and speed (0.00,0.00,2.82)
*********** Physical computations end ************

11.8.2. Protein Data Bank

On chercher a réaliser un script qui analyse un fichier de données de type Protein Data Bank.

La banque de données Worldwide Protein Data Bank regroupe les structures obtenues par diffraction aux rayons X ou par RMN. Le format est parfaitement defini et conventionnel (documentation).

On propose d’assurer une lecture de ce fichier pour calculer notamment :

• le barycentre de la biomolécule

• le nombre d’acides aminés ou nucléobases

• le nombre d’atomes

• la masse moléculaire

• les dimensions maximales de la protéine

• etc.

On propose de considerer par exemple la structure resolue pour la GFP (Green Fluorescent Protein, Prix Nobel 2008) (Fichier PDB)