13. Projets🔗

13.1. Projets de physique🔗

13.1.1. Formation d’agrégats🔗

La formation d’agrégats est par essence un sujet interdisciplinaire, ou la modélisation joue un rôle certain comme « microscope computationel ». Pour un projet en ce sens, un soin particulier sera donné à la contextualisation. P.ex., on pourra tester les limites de la règle de Wade pour la structure de clusters métalliques, ou bien dans un contexte plus biologique.

../_images/DLA.jpg

Fig. 13.1 Figure: Résultat d’une agrégation limitée par la diffusion d’environ 33 000 particules obtenue en permettant à des marcheurs aléatoires d’adhérer à une semence centrale. Les couleurs indiquent le temps d’arrivée des marcheurs. Source: WingkLEE (Own work) [Public domain], via Wikimedia Commons.🔗

13.1.2. Modèle d’Ising🔗

Le modèle d’Ising est le modèle le plus simple du magnétisme. Le modèle 1D est exactement soluble par la méthode de la matrice de transfert. La généralisation à 2 dimensions a été faite par Lars Onsager en 1944, mais la solution est assez compliquée. Il n’existe pas de solution analytique en 3D. On va ici considérer un système de spins sur réseau. Chaque spin \(\sigma_i\) peut prendre 2 valeurs (« up » et « down »). L’hamiltonien du système,

\[H = -J \sum_{i,j} \sigma_i \sigma_j - h \sum_{i} \sigma_i\]

contient deux contributions : l’interaction entre premiers voisins et le couplage à un champ magnétique. On va considérer un réseau carré avec une interaction ferromagnétique (\(J > 0\)). L’objectif du projet sera d’étudier le diagramme de phase du système en fonction de la température et du champ magnétique par simulation de Monte-Carlo.

../_images/ising.png

Fig. 13.2 Figure: Modèle d’Ising au point critique.🔗

13.1.3. Modèle de Potts 3D🔗

Modèle de Potts en 3D dans un univers carré à condition périodique. Le but est la mise en évidence de la transition de phase pour plusieurs jeux de paramètres avec 3 types de spins différents.

  1. Reproduire des résultats connus du modèle d’Ising en 2D pour valider le code.

  2. Passer à un algorithme en cluster pour évaluer la différence avec un algorithme classique.

  3. Passer en 3D

  4. Changer le nombre de type de spins (de 2 à 3).

Jeux de paramètres à tester :

  • Ising en 2D (2 types de spins, algorithme de Glauber): Transition de phase attendue à T~227K pour un couplage J=100 et un champ externe nul

  • Toujours Ising, mais avec l”algorithme de Wolff

  • Ising en 3D avec Wolff

  • Potts (changer q=2 par q=3) en 3D avec Wolff

Références:

Computational Studies of Pure and Dilute Spin Models

13.1.4. Méthode de Hückel🔗

La spectroscopie et la réactivité des électrons \(\pi\) est centrale en chimie. Un outil efficace pour les appréhender est l’approche développé par Hückel. Il vous est demande ici de mettre en oeuvre cette méthode pour l’analyse des orbitales et de l’énergie d’une famille de molécules répondant aux hypothèse sous-jacentes. On discutera notamment du choix de la paramétrisation du système.

13.1.5. Densité d’états d’un nanotube🔗

Les nanotubes de carbone ont été découverts bien avant celle du graphène. Ce sont des matériaux très résistants et durs qui possèdent une conductivité électrique et thermique élevées. Un nanotube de carbone monofeuillet consiste d’une couche de graphène enroulé selon un certain axe. L’axe d’enroulement détermine la chiralité du nanotube et, par la suite, les propriétés électroniques : selon la chiralité, le nanotube peut être soit semi-conducteur, soit métallique. L’objectif du projet sera de calculer la densité d’états de nanotubes de carbone de différentes chiralités et d’établir le lien entre la chiralité et le fait que le nanotube soit semiconducteur ou métallique.

13.1.6. Solitons🔗

On considère un câble sous tension auquel sont rigidement et régulièrement attachés des pendules. Les pendules sont couplés grâce au câble à travers sa constante de torsion. Dans un tel système on peut observer une large gamme de phénomènes ondulatoires. Le but de cet projet est d’étudier une solution très particulière : le soliton.

Imaginons qu’une des extrémités du câble est attachée à une manivelle qui peut tourner librement. Il est alors possible de donner une impulsion au système en faisant un tour rapide ce qui déclenche la propagation d’un soliton. Dans ce projet, on considérera les pendules individuellement. Il n’est pas demandé de passer au modèle continu et de résoudre l’équation obtenue.

Pour chaque pendule n dont la position est décrite par \(\theta_n\), l’équation d’évolution s’écrit:

\[\frac{d^2\theta_n}{d t^2} = \alpha\sin\theta_n + \beta(\theta_{n-1} + \theta_{n+1} - 2\theta_n)\]

où \(\alpha,\beta\) sont des paramètres physiques. On résoudra numériquement cette équation pour chaque pendule. En donnant un « tour de manivelle numérique », on essayera d’obtenir la solution soliton. On cherchera en particulier à ajuster la solution par une équation du type \(\theta_n = a \tan^{-1}(\exp(b(n-n_0)))\) où \(a,b,n_0\) sont des paramètres à déterminer.

De très nombreuses questions se posent (il ne vous est pas demandé de répondre à chacune d’entre elle):

  • Est-il toujours possible d’obtenir un soliton?

  • Sa vitesse est-elle constante?

  • Le soliton conserve-t-il sa forme?

  • Que se passe-t-il avec des pendules plus lourds? ou plus rapprochés? avec un câble plus rigide? avec un frottement?

  • Comment le soliton se réfléchit-il si l’extrémité du câble est rigidement fixée? et si elle tourne librement?

  • Dans ce système, le soliton est chiral. En effet, on peut tourner la manivelle à gauche ou à droite. Un anti-soliton a-t-il les mêmes propriétés (taille, vitesse, énergie) qu’un soliton?

  • Si on place une manivelle à chaque extrémité, on peut faire se collisionner des solitons. Cette étude est très intéressante et pleine de surprises. Que se passe-t-il lors de la collision de deux solitons? Entre un soliton et un anti-soliton?

../_images/mascaret.jpg

Fig. 13.3 Figure: Un mascaret, une vague soliton, dans un estuaire de Grande Bretagne. Source: Arnold Price [CC-BY-SA-2.0], via Wikimedia Commons.🔗

13.1.7. Diagramme de phase du potentiel de Lennard-Jones🔗

Auteur de la section : Mathieu Leocmach <mathieu.leocmach@ens-lyon.fr>

Le potentiel de Lennard-Jones est souvent utilisé pour décrire les interactions entre deux atomes au sein d’un système monoatomique de type gaz rare. Son expression en fonction de la distance r entre les deux noyaux atomiques est :

\[E_p(r) = 4 E_0 \left[ \left( \frac{r_0}{r} \right)^{12} - \left( \frac{r_0}{r} \right)^{6} \right]\]

avec \(r_0\) la distance pour laquelle \(E_p(r_0) = 0\).

On programmera un simulateur de dynamique moléculaire pour N particules identiques dans un cube periodique de taille fixe L et à une température T. On prendra soin d’adimentionner toutes les grandeurs et d’imposer des conditions aux limites periodiques. On se renseignera sur les façons possibles de déterminer les conditions initiales et d’imposer la température.

Les positions et vitesses des particules seront exportées de façon régulières pour visualisation (par exemple dans Paraview).

  • On pourra observer les collisions de 2 ou 3 particules à différentes températures avant de passer à des N plus grands (100 particules?).

  • On fera varier \(V=L^3\) et T pour déterminer les frontières des différentes phases.

  • On pourra aussi essayer d’aller vers de plus grands N pour tester l’influence de la taille finie de l’échantillon. Des optimisations seront alors sûrement nécessaires pour accélérer le programme.

  • On pourra aussi tester d’autres types de potentiels comme celui de Weeks-Chandler-Anderson et discuter des différences observées.

13.1.8. États de diffusion pour l’équation de Schrödinger 1D stationnaire🔗

On s’intéresse à la diffusion d’une particule de masse m à travers un potentiel carré défini par \(V(x) = V_0\) pour \(0 \leq x \leq a\), et 0 sinon.

Les solutions de cette équation en dehors de la région où règne le potentiel sont connues. Les paramètres d’intégration de ces fonctions d’onde peuvent se déterminer par les relations de continuité aux frontières avec la région où règne le potentiel. En résolvant l’équation différentielle dans la région du potentiel pour x allant de a à 0 on peut obtenir une autre valeur pour ces paramètre d’intégration. Il faut ensuite appliquer un algorithme de minimisation pour déterminer les constantes d’intégration.

Les objectifs de ce projet sont :

  • Écrire un programme qui résolve l’équation de Schrödinger.

  • En déduire les coefficients de transmission et de réflexion.

Références:

13.1.9. Percolation🔗

Ce sujet propose d’étudier le phénomène de percolation. La percolation est un processus physique qui décrit pour un système, une transition d’un état vers un autre. Le système que nous étudierons est composé ici d’une grille carrée dont les cases sont soit vides, soit pleines. Initialement, la matrice est vide et l’on tire aléatoirement une case que l’on rempli. On défini la concentration comme le rapport du nombre de cases noires sur le nombre total de cases. À partir d’une certaine concentration critique un chemin continu de cases noires s’établit entre deux bords opposés du système (haut et bas, ou gauche et droite) et on dit alors que le système percole. Le but du sujet est d’étudier la transition d’un système qui ne percole pas (à gauche sur la figure) vers un système qui percole (à droite). Pour ce faire, on établira un algorithme qui pour une configuration donnée détermine si le réseau de cases noires percole ou non. On étudiera également la taille et le nombre des amas de cases noires en fonction de la concentration. On étudiera aussi les effets de la taille du système.

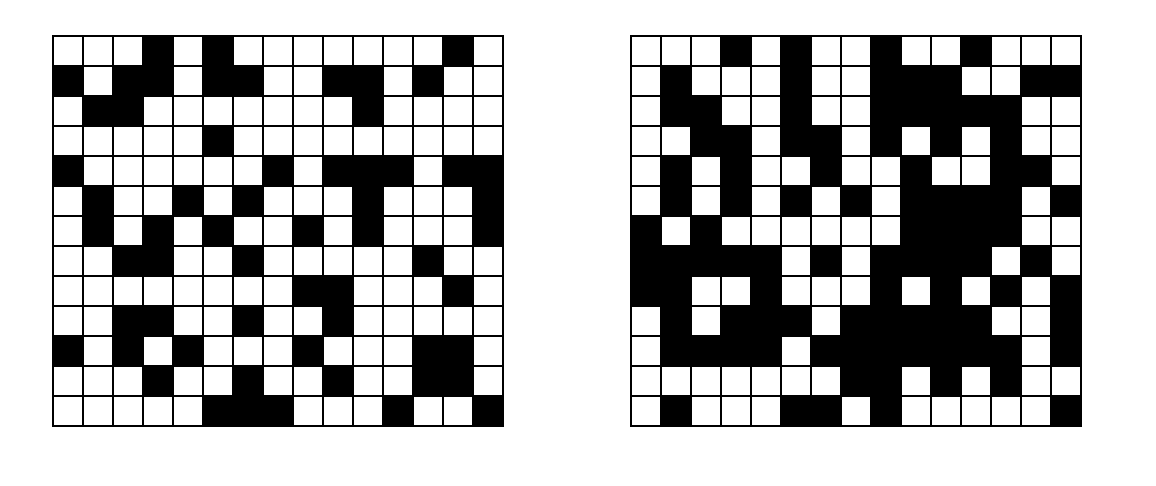
../_images/percolation.png

Cette étude repose sur un tirage pseudo aléatoire et pas conséquent nécessite un traitement statistique. On ne pourra pas se contenter d’étudier un cas particulier mais on prendra soin au contraire d’effectuer des moyennes sur un très grand nombre de tirages (plusieurs centaines).

Références:

13.2. Projets astrophysiques🔗

Auteur de la section : Méthodes numériques pour la physique et les SPI

13.2.1. Relation masse/rayon d’une naine blanche🔗

D’après la théorie de l’évolution stellaire, les naines blanches sont l’un des états possibles d’une étoile (peu massive) à la fin de sa vie, lorsque les réactions de fusion thermonucléaire s’arrêtent.

En première approximation un corps astrophysique est essentiellement soumis à la force de gravitation (qui tend à le contracter) et une force interne de pression qui vient équilibrer la première. Ainsi on peut approcher le problème par un équilibre hydrostatique caractérisé par :

\[\boldsymbol{\nabla} P(r) = - \rho(r) \frac{GM(r)}{r^2}\boldsymbol{e}_r\]

où G est la constante de gravitation, \(P(r)\), \(\rho(r)\) et \(M(r)\) respectivement la pression, la densité à la distance r du centre et la masse dans une sphère de rayon r.

Il s’agit d’étudier ici quelle force peut équilibrer la gravitation pour une naine blanche et mettre en évidence une masse limite en étudiant la relation rayon/masse.

Modélisation

La masse et le rayon d’équilibre de ce système sont entièrement déterminés par l’équation d’état thermodynamique \(P = P(\rho)\) et la densité centrale. En effet on montre facilement que :

\[\begin{split}\frac{d \rho}{dr} &= - { \left( \frac{dP}{d \rho} \right) }^{-1} \frac{GM}{r^2} \rho \\ \frac{dM}{dr} &= 4\pi r^2\rho\end{split}\]

Une fois que les réactions thermonucléaires s’arrêtent, la première des forces empêchant l’étoile de s’effondrer vient de la pression due aux électrons. Le modèle que nous utiliserons sera donc un simple gaz d’électrons (masse \(m_e\) et de nombre par unité de volume n) plongé dans un gaz de noyaux (on note \(Y_e\) le nombre d’électrons par nucléon et \(M_n\) la masse d’un nucléon) d’équation d’état :

\[\begin{split}\frac{E}{V} &= n_0 m_ec^2 x^3 \varepsilon (x), \\ \text{avec}\quad x &= {\left( \frac {\rho}{\rho_0} \right) }^{\frac{1}{3}}, \\ n_0 &= \frac{{m_e^3c^3}}{3\hbar^3 \pi^2}, \\ \rho_0 &= \frac{M_n n_0}{Y_e} \\ \text{et}\quad \varepsilon(x) &= \frac{3}{8 x^3} \left[ x(1 + 2x^2) \sqrt{1 + x^2} - \ln \left( x + \sqrt{1 + x^2}\right) \right]\end{split}\]

Si tous les noyaux sont du \(^{12}C\), alors \(Y_e=1/2\).

  1. Montrer que le système d’équations à résoudre est

    \[\begin{split}\frac{d \rho}{dr} &= - { \left( \frac{3M_n G}{Y_e m_ec^2}\frac{\sqrt{1+x^2}}{x^2}\right) } \frac{M}{r^2} \rho \\ \frac{dM}{dr} &= 4\pi r^2\rho\end{split}\]

  2. En fixant la densité centrale \(\rho(r=0)=\rho_c\) tracer \(\rho(r)\) et en déduire une méthode pour calculer le rayon R de l’étoile et sa masse M.

  3. En faisant varier la densité centrale tracer la relation \(M(R)\).

  4. Discuter la validité numérique et physique des résultats par exemple en changeant la composition de l’étoile, la définition du rayon de l’étoile, etc.

13.2.2. Section de Poincaré🔗

Les équations du mouvement 1 \(\boldsymbol{r}(t) = (x(t),y(t))\) d’une particule de masse \(m\) plongée dans un potentiel \(\Phi(x,y)\) s’écrivent:

\[m\ddot{\boldsymbol{r}} = -\nabla\Phi.\]

En coordonnées polaires :

\[\begin{split}a_r &= \ddot{r} - r\dot{\theta}^2 = -\frac{1}{m}\frac{\partial\Phi}{\partial r} \\ a_{\theta} &= 2\dot{r}\dot{\theta}+r\ddot{\theta} = -\frac{1}{mr}\frac{\partial\Phi}{\partial \theta}\end{split}\]

Le système peut donc s’écrire :

\[\begin{split}\ddot{r} &= r\dot{\theta}^2 -\frac{1}{m}\frac{\partial\Phi}{\partial r} \\ \ddot{\theta} &= -\frac{2}{r}\dot{r}\dot{\theta}-\frac{1}{mr^2} \frac{\partial\Phi}{\partial\theta}\end{split}\]

ou en posant \(r_p=\dot{r}\) et \(\theta_p=\dot{\theta}\):

\[\begin{split}\dot{r} &= r_p \\ \dot{\theta} &= \theta_p \\ \dot{r_p} &= r\theta_p^2 -\frac{1}{m}\frac{\partial\Phi}{\partial r} \\ \dot{\theta_p} &= -\frac{2}{r}r_p\theta_p-\frac{1}{mr^2}\frac{\partial\Phi}{\partial\theta}\end{split}\]

L’intégration – analytique ou numérique – de ces équations pour des conditions initiales \((\boldsymbol{r}(t=0),\dot{\boldsymbol{r}}(t=0))\) particulières caractérise une orbite. Le tracé de l’ensemble des points d’intersection de différentes orbites de même énergie avec le plan, p.ex., \((x,\dot{x})\) (avec \(y=0\) et \(\dot{y}>0\)) constitue une section de Poincaré.

Nous étudierons plus particulièrement le cas particulier \(m=1\) et les deux potentiels:

  1. le potentiel intégrable de Sridhar & Touma (1997; MNRAS, 287, L1) 2, qui s’exprime naturellement dans les coordonnées polaires \((r,\theta)\):

    \[\label{eq:spST} \Phi(r,\theta) = r^{\alpha}\, \left[(1+\cos\theta)^{1+\alpha} + (1-\cos\theta)^{1+\alpha}\right].\]

    avec p.ex. \(\alpha = 1/2\);

  2. le potentiel de Hénon-Heiles:

    \[\label{eq:spHH} \Phi(r,\theta) = \frac{1}{2}r^2 + \frac{1}{3}r^3\sin(3\theta).\]

Objectif

  1. Écrire un intégrateur numérique permettant de résoudre les équations du mouvement pour un potentiel et des conditions initiales données.

  2. Les performances de cet intégrateur seront testées sur des potentiels intégrables (p.ex. potentiel képlerien \(\Phi \propto 1/r\)), ou en vérifiant la stabilité des constantes du mouvement (l’énergie \(E = \frac{1}{2}\dot{\boldsymbol{r}}^{2} + \Phi\)).

  3. Pour chacun des potentiels, intégrer et stocker une grande variété d’orbites de même énergie, en prenant soin de bien résoudre la zone d’intérêt autour de \((y=0,\dot{y}>0)\).

  4. À l’aide de fonctions d’interpolation et de recherche de zéro, déterminer pour chacune des orbites les coordonnées \((x,\dot{x})\) de l’intersection avec le plan \((y=0,\dot{y}>0)\).

  5. Pour chacun des potentiels, regrouper ces points par orbite pour construire la section de Poincaré de ce potentiel.

1

On se place dans toute la suite du problème dans un espace à deux dimensions.

2

Nous utiliserons toutefois les notations de l’appendice de Copin, Zhao & de Zeeuw (2000; MNRAS, 318, 781).

13.3. Projets divers🔗

13.3.1. Formation de pistes de fourmis sur un pont à 2 branches🔗

Si on propose à une colonie de fourmis de choisir entre 2 branches pour rejoindre une source de nourriture la branche finalement choisie est toujours la plus courte. Le projet consiste à modéliser et caractériser ce comportement.

Indication: on peut étudier ce système avec des EDOs. Cela peut aussi donner lieu à une simulation individu centré et éventuellement une comparaison entre les deux types de modèle.

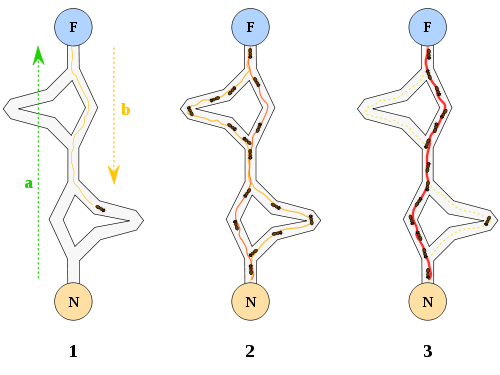
../_images/Aco_branches.png

Fig. 13.4 Figure: 1) la première fourmi trouve la source de nourriture (F), via un chemin quelconque (a), puis revient au nid (N) en laissant derrière elle une piste de phéromone (b). 2) les fourmis empruntent indifféremment les 4 chemins possibles, mais le renforcement de la piste rend plus attractif le chemin le plus court. 3) les fourmis empruntent le chemin le plus court, les portions longues des autres chemins voient la piste de phéromones s’évaporer. Source: Johann Dréo via Wikimedia Commons.🔗

13.3.2. Auto-organisation d’un banc de poisson🔗

Auteur de la section : Hanna Julienne <hanna.julienne@gmail.com>

La coordination d’un banc de poissons ou d’un vol d’oiseaux est tout à fait frappante: les milliers d’individus qui composent ces structures se meuvent comme un seul. On observe aussi, dans les bancs de poisson, d’impressionnants comportements d’évitement des prédateurs (flash expansion, fountain effect).

Pourtant ces mouvements harmonieusement coordonnés ne peuvent pas s’expliquer par l’existence d’un poisson leader. Comment pourrait-il être visible par tous ou diriger les flash expansion qui ont lieu à un endroit précis du banc de poisson? De la même manière on ne voit pas quelle contrainte extérieure pourrait expliquer le phénomène.

Une hypothèse plus vraisemblable pour rendre compte de ces phénomènes est que la cohérence de l’ensemble est due à la somme de comportements individuels. Chaque individu adapte son comportement par rapport à son environnement proche. C’est ce qu’on appelle auto-organisation. En effet, on a établi expérimentalement que les poissons se positionnent par rapport à leurs k plus proches voisins de la manière suivante:

  • ils s’éloignent de leurs voisins très proches (zone de répulsion en rouge sur la figure ci-dessous)

  • ils s’alignent avec des voisins qui sont à distance modérée (zone jaune)

  • ils s’approchent de leur voisins s’ils sont à la fois suffisamment proches et distants (zone verte)

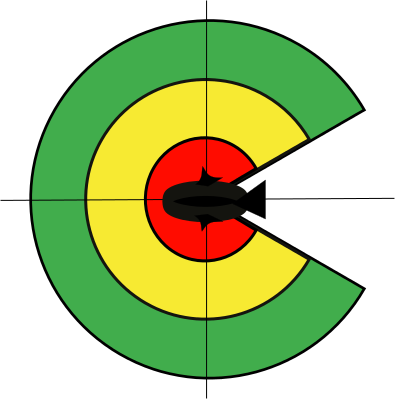
../_images/zone_poisson.png

Fig. 13.5 Figure: Environnement proche du poisson: zones dans lesquelles le positionnement d’un voisin provoque une réponse de la part de l’individu au centre🔗

Dans notre modèle, nous allons prendre en compte l’influence des k plus proches voisins. On calculera la contribution de chaque voisin selon la zone dans laquelle il se situe. Le déplacement du poisson sera la moyenne de ces contributions. Il est à noter qu’un voisin en dehors des trois zones d’influence n’a pas d’effet.

L’environnement proche d’un poisson est modélisé par des sphères imbriquées qui présentent une zone aveugle (voir figure).

Par ailleurs, si un individu n’a pas de voisins dans son environnement proche il adopte un comportment de recherche. Il explore aléatoirement les alentours jusqu’à ce qu’il repère le banc de poissons et finalement s’en rapproche.

Ce projet vise à :

  • Coder le comportement des poissons et à les faire évoluer dans un environnement 2D.

  • On essaiera d’obtenir un comportement collectif cohérent (similaire à un banc de poisson) et d’établir les conditions nécessaires à ce comportement.

  • On étudiera notamment l’influence du nombre d’individus pris en compte. Est-ce que le positionnement par rapport au plus proche voisin (k = 1) est suffisant?

  • On pourra se servir de la visualisation pour rendre compte de la cohérence du comportment et éventuellement inventer des mesures pour rendre compte de manière quantifier de cette cohérence.

Liens :

13.3.3. Évacuation d’une salle & déplacement d’une foule dans une rue🔗

Le comportement d’une foule est un problème aux applications multiples: évacuation d’une salle, couloir du métro aux heures de pointes, manifestations… On peut en imaginer des modèles simples. P. ex., on peut décrire chaque individu par sa position, sa vitesse, et comme étant soumis à des « forces »:

  • Une force qui spécifie la direction dans laquelle l’individu veut se déplacer, \(\textbf{f}_{dir} = (\textbf{v}_0 - \textbf{v}(t))/\tau\), où \(\textbf{v}_0\) est la direction et la vitesse que la personne veut atteindre, \(\textbf{v}\) sa vitesse actuelle, et \(\tau\) un temps caractéristique d’ajustement.

  • Une force qui l’oblige à éviter des obstacles qui peuvent être fixes (un mur, un massif de fleurs, …), ou qui peuvent être les autres individus eux-mêmes. On pourra essayer \(f_{obs}(d) = a \exp(-d/d_0)\), où \(d\) est la distance entre le piéton et l’obstacle, \(d_0\) la « portée » de la force, et \(a\) son amplitude.

On pourra varier les différents paramètres apparaissant ci-dessus, tout en leur donnant une interprétation physique réelle, et étudier leur influence dans des situations concrètes. P. ex., à quelle vitesse, en fonction de \(\textbf{v}_0\) et de la densité de piétons, se déplace une foule contrainte à avancer dans un couloir si chaque individu veut maintenir une vitesse \(\textbf{v}_0\) ? Comment s’organise l’évacuation d’une salle initialement uniformément peuplée, avec une ou plusieurs sorties, et en la présence éventuels d’obstacles ?

Il est également possible d’essayer d’autres expressions pour les forces.

Il existe une littérature conséquente sur le sujet, que l’on pourra explorer si besoin (p. ex: Décrypter le mouvement des piétons dans une foule).

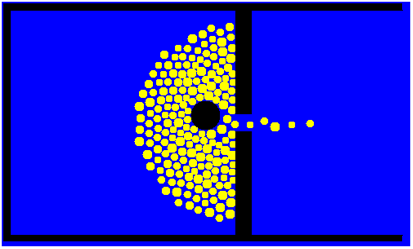
../_images/6k-RoomExit4.png

Fig. 13.6 Figure: Un obstacle aide à l’évacuation (DR).🔗

13.3.4. Suivi de particule(s)🔗

Auteur de la section : Mathieu Leocmach <mathieu.leocmach@ens-lyon.fr>

Dans de nombreux domaines de recherche expérimentale, on a besoin de localiser des particles dans une image ou de reconstituer leurs trajectoires à partir d’une vidéo. Il peut s’agir de virus envahissant une cellule, de traceurs dans un écoulement, d’objets célestes fonçant vers la terre pour la détruire, etc.

Dans ce projet, on essayera d’abord de localiser une particule unique dans une image à 2 dimensions (niveaux de gris) en utilisant l’algorithme de Crocker & Grier décrit ici. On utilisera sans retenue les fonctions de la bibliothèque scipy.ndimage.

On essayera d’obtenir une localisation plus fine que la taille du pixel. On essayera ensuite de détecter plusieurs particules dans une image.

Afin de pouvoir traiter efficacement une séquence d’images de même taille, on privilégiera une implémentation orientée objet. L’objet de la classe Finder sera construit une seule fois en début de séquence et il contiendra les images intermédiaires nécessaire au traitement. On nourrira ensuite cet objet avec chaque image de la séquence pour obtenir les coordonnées des particules.

Enfin, on pourra essayer de relier les coordonnées dans des images successives pour constituer des trajectoires.

On contactera le créateur du sujet pour obtenir des séquences d’images expérimentales de particules Browniennes.

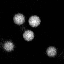
../_images/dilute_raw.png

Fig. 13.7 Figure: Exemple d’image test où on voudra localiser les particules.🔗

13.5. Projets de visualisation🔗

L’objectif premier de ces projets est de développer des outils de visualisation sous Python/Matplotlib.