6. Bibliothèques numériques de base🔗
Table des matières
6.1. Numpy🔗
numpy est une bibliothèque numérique apportant le support
efficace de larges tableaux multidimensionnels, et de routines
mathématiques de haut niveau (fonctions spéciales, algèbre linéaire,
statistiques, etc.).
Note
La convention d’import utilisé dans les exemples est «
import numpy as N».N’oubliez pas de citer numpy dans vos publications et présentations utilisant ces outils.
Liens:
6.1.1. Tableaux🔗
Un numpy.ndarray (généralement appelé array) est un tableau
multidimensionnel homogène: tous les éléments doivent avoir le même
type, en général numérique. Les différentes dimensions sont appelées
des axes, tandis que le nombre de dimensions – 0 pour un scalaire,
1 pour un vecteur, 2 pour une matrice, etc. – est appelé le rang.
>>> import numpy as N # Import de la bibliothèque numpy avec le surnom N
>>> a = N.array([1, 2, 3]) # Création d'un array 1D à partir d'une liste d'entiers
>>> a.ndim # Rang du tableau
1 # Vecteur (1D)
>>> a.shape # Format du tableau: par définition, len(shape)=ndim
(3,) # Vecteur 1D de longueur 3
>>> a.dtype # Type des données du tableau
dtype('int32') # Python 'int' = numpy 'int32' = C 'long'
>>> # Création d'un tableau 2D de float (de 0. à 12.) de shape 4×3
>>> b = N.arange(12, dtype=float).reshape(4, 3); b
array([[ 0., 1., 2.],
[ 3., 4., 5.],
[ 6., 7., 8.],
[ 9., 10., 11.]])
>>> b.shape # Nb d'éléments le long de chacune des dimensions
(4, 3) # 4 lignes, 3 colonnes
>>> b.size # Nb *total* d'éléments dans le tableau
12 # Par définition, size = prod(shape)
>>> b.dtype
dtype('float64') # Python 'float' = numpy 'float64' = C 'double'
6.1.1.1. Création de tableaux🔗
numpy.array(): convertit une liste d’éléments homogènes ou coercibles>>> N.array([[1, 2],[3., 4.]]) # Liste de listes d'entiers et de réels array([[ 1., 2.], # Tableau 2D de réels [ 3., 4.]])
numpy.zeros()(resp.numpy.ones()etnumpy.full()): crée un tableau de format donné rempli de zéros (resp. de uns et d’une valeur fixe)>>> N.zeros((2, 1)) # Shape (2, 1): 2 lignes, 1 colonne, float par défaut array([[ 0.], [ 0.]]) >>> N.ones((1, 2), dtype=bool) # Shape (1, 2): 1 ligne, 2 colonnes, type booléen array([[True, True]], dtype=bool) >>> N.full((2, 2), N.NaN) array([[ nan, nan], [ nan, nan]])
numpy.arange(): crée une séquence de nombres, en spécifiant éventuellement le start, le end et le step (similaire àrange()pour les listes)>>> N.arange(10, 30, 5) # De 10 à 30 (exclu) par pas de 5, type entier par défaut array([10, 15, 20, 25]) >>> N.arange(0.5, 2.1, 0.3) # Accepte des réels en argument, DANGER! array([ 0.5, 0.8, 1.1, 1.4, 1.7, 2. ])
numpy.linspace()(resp.numpy.logspace()): répartition uniforme (resp. logarithmique) d’un nombre fixe de points entre un start et un end (préférable ànumpy.arange()sur des réels).>>> N.linspace(0, 2*N.pi, 5) # 5 nb entre 0 et 2π *inclus*, type réel par défaut array([ 0., 1.57079633, 3.14159265, 4.71238898, 6.28318531]) >>> N.logspace(-1, 1, 5) # 5 nb répartis log. entre 10**(±1) array([ 0.1 , 0.31622777, 1. , 3.16227766, 10. ])
numpy.meshgrid()est similaire ànumpy.linspace()en 2D ou plus:>>> # 5 points entre 0 et 2 en "x", et 3 entre 0 et 1 en "y" >>> x = N.linspace(0, 2, 5); x # Tableau 1D des x, (5,) array([ 0. , 0.5, 1. , 1.5, 2. ]) >>> y = N.linspace(0, 1, 3); y # Tableau 1D des y, (3,) array([ 0. , 0.5, 1. ]) >>> xx, yy = N.meshgrid(x, y) # Tableaux 2D des x et des y >>> xx # Tableau 2D des x, (3, 5) array([[ 0. , 0.5, 1. , 1.5, 2. ], [ 0. , 0.5, 1. , 1.5, 2. ], [ 0. , 0.5, 1. , 1.5, 2. ]]) >>> yy # Tableau 2D des y, (3, 5) array([[ 0. , 0. , 0. , 0. , 0. ], [ 0.5, 0.5, 0.5, 0.5, 0.5], [ 1. , 1. , 1. , 1. , 1. ]])
Index tricks
numpy.r_(resp.numpy.c_) est un opérateur puissant avec une notation évoluée (index tricks), permettant à la fois la génération (équivalent ànumpy.arange()etnumpy.linspace()) et la concaténation (numpy.concatenate()) le long du 1e axe (resp. du 2e axe):>>> N.concatenate([[0], N.arange(1, 6, 2), N.zeros(2), N.linspace(1, 2, 3)]) array([0. , 1. , 3. , 5. , 0. , 0. , 1. , 1.5, 2. ]) >>> N.r_[0, 1:6:2, [0]*2, 1:2:3j] # Notez les crochets et les slices array([0. , 1. , 3. , 5. , 0. , 0. , 1. , 1.5, 2. ]) >>> N.c_[1:6:2, 1:2:3j] array([[1. , 1. ], [3. , 1.5], [5. , 2. ]])
Plus généralement,
numpy.mgridpermet de générer des rampes d’indices (entiers) ou de coordonnées (réels) de rang arbitraire avec les index tricks. Équivalent ànumpy.linspace()en 1D et similaire (mais différent) ànumpy.meshgrid()en 2D.>>> N.mgrid[0:4, 1:6:2] # Grille 2D d'indices (entiers) array([[[0, 0, 0], # 0:4 = [0, 1, 2, 3] selon l'axe 0 [1, 1, 1], [2, 2, 2], [3, 3, 3]], [[1, 3, 5], # 1:6:2 = [1, 3, 5] selon l'axe 1 [1, 3, 5], [1, 3, 5], [1, 3, 5]]]) >>> N.mgrid[0:2*N.pi:5j] # Rampe de coordonnées (réels): 5 nb de 0 à 2π (inclus) array([ 0., 1.57079633, 3.14159265, 4.71238898, 6.28318531]) >>> # 3 points entre 0 et 1 selon l'axe 0, et 5 entre 0 et 2 selon l'axe 1 >>> z = N.mgrid[0:1:3j, 0:2:5j]; z array([[[ 0. , 0. , 0. , 0. , 0. ], # Axe 0 variable, axe 1 constant [ 0.5, 0.5, 0.5, 0.5, 0.5], [ 1. , 1. , 1. , 1. , 1. ]], [[ 0. , 0.5, 1. , 1.5, 2. ], # Axe 0 constant, axe 1 variable [ 0. , 0.5, 1. , 1.5, 2. ], [ 0. , 0.5, 1. , 1.5, 2. ]]]) >>> z.shape (2, 3, 5) # 2 plans 2D (y, x) de 3 lignes (y) × 5 colonnes (x) >>> N.mgrid[0:1:5j, 0:2:7j, 0:3:9j].shape (3, 5, 7, 9) # 3 volumes 3D (z, y, x) de 5 plans (z) × 7 lignes (y) × 9 colonnes (x)
numpy.ogridest similaire ànumpy.mgridmais permet de générer des rampes d’indices ou de coordonnées compactes (sparse):>>> N.ogrid[0:4, 1:6:2] # Rampes 2D d'indices (entiers) [array([[0], [1], [2], [3]]), array([[1, 3, 5]])]
Attention
à l’ordre de variation des indices dans les tableaux multidimensionnels, et aux différences entre
numpy.meshgrid()etnumpy.mgrid/numpy.ogrid.
Tableaux aléatoires
numpy.random.rand()crée un tableau d’un format donné de réels aléatoires dans [0, 1[;numpy.random.randn()génère un tableau d’un format donné de réels tirés aléatoirement d’une distribution gaussienne (normale) standard \(\mathcal{N}(\mu=0, \sigma^2=1)\).
6.1.1.2. Manipulations sur les tableaux🔗
Les array 1D sont indexables comme les listes standard. En dimension
supérieure, chaque axe est indéxable indépendamment.
>>> x = N.arange(10); # Rampe 1D
>>> x[1::3] *= -1; x # Modification sur place ("in place")
array([ 0, -1, 2, 3, -4, 5, 6, -7, 8, 9])
Slicing
Les sous-tableaux de rang < N d’un tableau de rang N sont appelées slices: le (ou les) axe(s) selon le(s)quel(s) la slice a été découpée, devenu(s) de longueur 1, est (sont) éliminé(s).
>>> y = N.arange(2*3*4).reshape(2, 3, 4); y # 2 plans, 3 lignes, 4 colonnes
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
>>> y[0, 1, 2] # 1er plan (axe 0), 2e ligne (axe 1), 3e colonne (axe 2)
6 # Scalaire, shape *()*, ndim 0
>>> y[0, 1] # = y[0, 1, :] 1er plan (axe 0), 2e ligne (axe 1)
array([4, 5, 6, 7]) # Shape (4,)
>>> y[0] # = y[0, :, :] 1er plan (axe 0)
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]) # Shape (3, 4)
>>> y[0][1][2] # = y[0, 1, 2] en ~4× plus lent (slices successives)
6
>>> y[:, -1] # = y[:, 2, :] Dernière slice selon le 2e axe
array([[ 8, 9, 10, 11],
[20, 21, 22, 23]]) # Shape (2, 4)
>>> y[..., 0] # = y[:, :, 0] 1re slice selon le dernier axe
array([[ 0, 4, 8],
[12, 16, 20]]) # Shape (2, 3)
>>> # On peut vouloir garder explicitement la dimension "tranchée"
>>> y[..., 0:1] # 1re slice selon le dernier axe *en gardant le rang originel*
array([[[ 0],
[ 4],
[ 8]],
[[12],
[16],
[20]]])
>>> y[..., 0:1].shape
(2, 3, 1) # Le dernier axe a été conservé, il ne contient pourtant qu'un seul élément
Modification de format
numpy.ndarray.reshape() modifie le format d’un tableau sans
modifier le nombre total d’éléments:
>>> y = N.arange(6).reshape(2, 3); y # Shape (6,) → (2, 3) (*size* inchangé)
array([[0, 1, 2],
[3, 4, 5]])
>>> y.reshape(2, 4) # Format incompatible (*size* serait modifié)
ValueError: total size of new array must be unchanged
numpy.ndarray.ravel() « déroule » tous les axes et retourne un
tableau de rang 1:
>>> y.ravel() # Ordre C par défaut: *1st axis slowest, last axis fastest*
array([ 0, 1, 2, 3, 4, 5]) # Shape (2, 3) → (6,) (*size* inchangé)
>>> y.ravel('F') # Ordre Fortran: *1st axis fastest, last axis slowest*
array([0, 3, 1, 4, 2, 5])
numpy.ndarray.transpose() transpose deux axes, par défaut les
derniers (raccourci: numpy.ndarray.T):
>>> y.T # Transposition = y.transpose() (voir aussi *rollaxis*)
array([[0, 3],
[1, 4],
[2, 5]])
numpy.ndarray.squeeze() élimine tous les axes de dimension 1.
numpy.expand_dims() ajoute un axe de dimension 1 en position
arbitraire. Cela est également possible en utilisant notation slice
avec numpy.newaxis.
>>> y[..., 0:1].squeeze() # Élimine *tous* les axes de dimension 1
array([0, 3])
>>> N.expand_dims(y[..., 0], -1).shape # Ajoute un axe de dim. 1 en dernière position
(2, 1)
>>> y[:, N.newaxis].shape # Ajoute un axe de dim. 1 en 2de position
(2, 1, 3)
numpy.resize() modifie le format en modifiant le nombre total
d’éléments:
>>> N.resize(N.arange(4), (2, 4)) # Complétion avec des copies du tableau
array([[0, 1, 2, 3],
[0, 1, 2, 3]])
>>> N.resize(N.arange(4), (4, 2))
array([[0, 1],
[2, 3],
[0, 1],
[2, 3]])
Attention
N.resize(arr, shape) (complétion avec des copies de arr) est
différent de arr.resize(shape) (complétion avec des 0).
Exercice:
Stacking
>>> a = N.arange(5); a
array([0, 1, 2, 3, 4])
>>> N.hstack((a, a)) # Stack horizontal (le long des colonnes) = N.r_[a, a]
array([0, 1, 2, 3, 4, 0, 1, 2, 3, 4])
>>> N.vstack((a, a)) # Stack vertical (le long des lignes) = N.r_['0,2', a, a]
array([[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4]])
>>> N.dstack((a, a)) # Stack en profondeur (le long des plans)
array([[[0, 0],
[1, 1],
[2, 2],
[3, 3],
[4, 4]]])
Broadcasting
L”array broadcasting définit les régles selon lesquelles deux tableaux de formats différents peuvent éventuellement s’apparier.
Deux tableaux de même rang sont compatibles (broadcastable) si, pour chaque axe, soit les tailles sont égales, soit l’une d’elles est exactement égale à 1. P.ex. (5, 3) et (1, 3) sont des formats broadcastable, (5, 3) et (5, 1) également, mais (5, 3) et (3, 1) ne le sont pas.
Si un tableau a un axe de taille 1, le tableau sera dupliqué à la volée autant de fois que nécessaire selon cet axe pour attendre la taille de l’autre tableau le long de cet axe. P.ex. un tableau (2, 1, 3) pourra être transformé en tableau (2, 5, 3) en le dupliquant 5 fois le long du 2e axe (
axis=1).La taille selon chaque axe après broadcast est égale au maximum de toutes les tailles d’entrée le long de cet axe. P.ex. (5, 3, 1) × (1, 3, 4) → (5, 3, 4).
Si un des tableaux a un rang (
ndim) inférieur à l’autre, alors son format (shape) est précédé d’autant de 1 que nécessaire pour atteindre le même rang. P.ex. (5, 3, 1) × (4,) = (5, 3, 1) × (1, 1, 4) → (5, 3, 4).
>>> a = N.arange(6).reshape(2, 3); a # Shape (2, 3)
array([[0, 1, 2],
[3, 4, 5]])
>>> b = N.array([10, 20, 30]); b # Shape (3,)
array([10, 20, 30])
>>> a + b # Shape (3,) ~ (1, 3) → (2, 3) = (1, 3) copié 2 fois
array([[10, 21, 32],
[13, 24, 35]]) # Shape (2, 3)
>>> c = N.array([10, 20]); c # Shape (2,)
array([10, 20])
>>> a + c # Shape (2,) ~ (1, 2) incompatible avec (2, 3)
ValueError: shape mismatch: objects cannot be broadcast to a single shape
>>> c[:, N.newaxis] # = c.reshape(-1, 1) Shape (2, 1)
array([[10],
[20]])
>>> a + c[:, N.newaxis] # Shape (2, 1) → (2, 3) = (2, 1) copié 3 fois
array([[10, 11, 12],
[23, 24, 25]])
Voir également cette présentation.
Indexation évoluée
>>> a = N.linspace(-1, 1, 5); a
array([-1. , -0.5, 0. , 0.5, 1. ])
>>> a >= 0 # Test logique: tableau de booléens
array([False, False, True, True, True], dtype=bool)
>>> (a >= 0).nonzero() # Indices des éléments ne s'évaluant pas à False
(array([2, 3, 4]),) # Indices des éléments >= 0
>>> a[(a >= 0).nonzero()] # Indexation par un tableau d'indices, pas pythonique :-(
array([ 0. , 0.5, 1. ])
>>> a[a >= 0] # Indexation par un tableau de booléens, pythonique :-D
array([ 0. , 0.5, 1. ])
>>> a[a < 0] -= 10; a # = N.where(a < 0, a - 10, a)
array([-11. , -10.5, 0. , 0.5, 1. ])
6.1.1.3. Opérations de base🔗
>>> a = N.arange(3); a # Shape (3,), type *int*
array([0, 1, 2])
>>> b = 1. # ~ Shape (), type *float*
>>> c = a + b; c # *Broadcasting*: () → (1,) → (3,)
array([ 1., 2., 3.]) # *Upcasting*: int → float
>>> a += 1; a # Modification *in place* (plus efficace si possible)
array([ 1., 2., 3.])
>>> a.mean() # *ndarray* dispose de nombreuses méthodes numériques de base
2.0
Opérations sur les axes
>>> x = N.random.permutation(6).reshape(3, 2); x # 3 lignes, 2 colonnes
array([[3, 4],
[5, 1],
[0, 2]])
>>> x.min() # Minimum global (comportement par défaut: `axis=None`)
0
>>> x.min(axis=0) # Minima le long de l'axe 0 (i.e. l'axe des lignes)
array([0, 1]) # ce sont les minima colonne par colonne: (*3*, 2) → (2,)
>>> x.min(axis=1) # Minima le long de l'axe 1 (i.e. l'axe des colonnes)
array([3, 1, 0]) # ce sont les minima ligne par ligne (3, *2*) → (3,)
>>> x.min(axis=1, keepdims=True) # Idem mais en *conservant* le format originel
array([[3],
[1],
[0]])
>>> x.min(axis=(0, 1)) # Minima le long des axes 0 *et* 1 (c.-à-d. ici tous les axes)
0
Opérations matricielles
Les opérations de base s’appliquent sur les éléments des tableaux, et n’ont pas une signification matricielle par défaut:
>>> m = N.arange(4).reshape(2, 2); m # Tableau de rang 2
array([[0, 1],
[2, 3]])
>>> i = N.identity(2, dtype=int); i # Tableau "identité" de rang 2 (type entier)
array([[1, 0],
[0, 1]])
>>> m * i # Attention! opération * sur les éléments
array([[0, 0],
[0, 3]])
>>> m @ i # Multiplication *matricielle* = N.dot(m, i): M × I = M
array([[0, 1],
[2, 3]])
Il est possible d’utiliser systématiquement les opérations
matricielles en manipulant des numpy.matrix plutôt que de
numpy.ndarray:
>>> N.matrix(m) * N.matrix(i) # Opération * entre matrices
matrix([[0, 1],
[2, 3]])
Le sous-module numpy.linalg fournit des outils spécifiques au
calcul matriciel (inverse, déterminant, valeurs propres, etc.).
Ufuncs
numpy fournit de nombreuses fonctions mathématiques de base
(numpy.exp(), numpy.atan2(), etc.) s’appliquant directement
sur les éléments des tableaux d’entrée:
>>> x = N.linspace(0, 2*N.pi, 5) # [0, π/2, π, 3π/2, 2π]
>>> y = N.sin(x); y # sin(x) = [0, 1, 0, -1, 0]
array([ 0.00000000e+00, 1.00000000e+00, 1.22460635e-16,
-1.00000000e+00, -2.44921271e-16])
>>> y == [0, 1, 0, -1, 0] # Test d'égalité stricte (élément par élément)
array([ True, True, False, True, False], dtype=bool) # Attention aux calculs en réels (float)!
>>> N.all(N.sin(x) == [0, 1, 0, -1, 0]) # Test d'égalité stricte de tous les éléments
False
>>> N.allclose(y, [0, 1, 0, -1, 0]) # Test d'égalité numérique de tous les éléments
True
Exercices:
6.1.2. Tableaux évolués🔗
Types composés
Par définition, tous les éléments d’un tableau homogène doivent être
du même type. Cependant, outre les types scalaires élémentaires –
bool, int, float, complex, str, etc. – numpy
supporte les types composés, c.-à-d. incluant plusieurs sous-éléments de
types différents:
>>> dt = N.dtype([('nom', 'U10'), # 1er élément: une chaîne de 10 caractères unicode
... ('age', 'i'), # 2e élément: un entier
... ('taille', 'd')]) # 3e élément: un réel (double)
>>> arr = N.array([('Calvin', 6, 1.20), ('Hobbes', 5, 1.80)], dtype=dt); arr
array([('Calvin', 6, 1.2), ('Hobbes', 5, 1.8)],
dtype=[('nom', '<U10'), ('age', '<i4'), ('taille', '<f8')])
>>> arr[0] # Accès par élément
('Calvin', 6, 1.2)
>>> arr['nom'] # Accès par sous-type
array(['Calvin', 'Hobbes'], dtype='<U10')
>>> rec = arr.view(N.recarray); rec # Vue de type 'recarray'
rec.array([('Calvin', 6, 1.2), ('Hobbes', 5, 1.8)],
dtype=[('nom', '<U10'), ('age', '<i4'), ('taille', '<f8')])
>>> rec.nom # Accès direct par attribut
array(['Calvin', 'Hobbes'], dtype='<U10')
Les tableaux structurés sont très puissants pour manipuler des données
(semi-)hétérogènes, p.ex. les entrées du catalogue CSV des objets de Messier Messier.csv:
1 2 3 4 5 6 7 8 | # Messier, NGC, Magnitude, Size [arcmin], Distance [pc], RA [h], Dec [deg], Constellation, Season, Name
# Attention: les données n'ont pas vocation à être très précises!
# D'après http://astropixels.com/messier/messiercat.html
M,NGC,Type,Mag,Size,Distance,RA,Dec,Con,Season,Name
M1,1952,Sn,8.4,5.0,1930.0,5.575,22.017,Tau,winter,Crab Nebula
M2,7089,Gc,6.5,12.9,11600.0,21.558,0.817,Aqr,autumn,
M3,5272,Gc,6.2,16.2,10400.0,13.703,28.383,CVn,spring,
M4,6121,Gc,5.6,26.3,2210.0,16.393,-26.533,Sco,summer,
|
>>> dt = N.dtype([('M', 'U3'), # N° catalogue Messier
... ('NGC', 'i'), # N° New General Catalogue
... ('Type', 'U2'), # Code type
... ('Mag', 'f'), # Magnitude
... ('Size', 'f'), # Taille [arcmin]
... ('Distance', 'f'), # Distance [pc]
... ('RA', 'f'), # Ascension droite [h]
... ('Dec', 'f'), # Déclinaison [deg]
... ('Con', 'U3'), # Code constellation
... ('Season', 'U6'), # Saison
... ('Name', 'U30')]) # Nom alternatif
>>> messier = N.genfromtxt("Messier.csv", dtype=dt, delimiter=',', comments='#')
>>> messier[1]
('M1', 1952, 'Sn', 8.39999962, 5., 1930., 5.57499981, 22.0170002, 'Tau', 'winter', 'Crab Nebula')
>>> N.nanmean(messier['Mag'])
7.4927273
Tableaux masqués
Le sous-module numpy.ma ajoute le support des tableaux masqués
(Masked Arrays). Imaginons un tableau (4, 5) de réels (positifs ou
négatifs), sur lequel nous voulons calculer pour chaque colonne la
moyenne des éléments positifs uniquement:
>>> x = N.random.randn(4, 5); x
array([[-0.55867715, 1.58863893, -1.4449145 , 1.93265481, -0.17127422],
[-0.86041806, 1.98317832, -0.32617721, 1.1358607 , -1.66150602],
[-0.88966893, 1.36185799, -1.54673735, -0.09606195, 2.23438981],
[ 0.35943269, -0.36134448, -0.82266202, 1.38143768, -1.3175115 ]])
>>> x[x >= 0] # Donne les éléments >0 du tableau, sans leur indice
array([ 1.58863893, 1.93265481, 1.98317832, 1.1358607 , 1.36185799,
2.23438981, 0.35943269, 1.38143768])
>>> (x >= 0).nonzero() # Donne les indices ([i], [j]) des éléments positifs
(array([0, 0, 1, 1, 2, 2, 3, 3]), array([1, 3, 1, 3, 1, 4, 0, 3]))
>>> y = N.ma.masked_less(x, 0); y # Tableau où les éléments <0 sont masqués
masked_array(data =
[[-- 1.58863892701 -- 1.93265481164 --] # Données
[-- 1.98317832359 -- 1.13586070417 --]
[-- 1.36185798574 -- -- 2.23438980788]
[0.359432688656 -- -- 1.38143767743 --]],
mask =
[[ True False True False True] # Bit de masquage
[ True False True False True]
[ True False True True False]
[False True True False True]],
fill_value = 1e+20)
>>> m0 = y.mean(axis=0); m0 # Moyenne sur les lignes (axe 0)
masked_array(data = [0.359432688656 1.64455841211 -- 1.48331773108 2.23438980788],
mask = [False False True False False],
fill_value = 1e+20) # Le résultat est un *Masked Array*
>>> m0.filled(-1) # Conversion en tableau normal
array([ 0.35943269, 1.64455841, -1. , 1.48331773, 2.23438981])
Note
Les tableaux évolués de numpy sont parfois
suffisants, mais pour une utilisation avancée, il peut être plus
pertinent d’invoquer les bibliothèques dédiées Pandas et xarray.
6.1.3. Entrées/sorties🔗
numpy peut lire – numpy.loadtxt() – ou sauvegarder –
numpy.savetxt() – des tableaux (uni- ou bi-dimensionnels) dans un simple
fichier ASCII:
>>> x = N.linspace(-1, 1, 100)
>>> N.savetxt('archive_x.dat', x) # Sauvegarde dans le fichier 'archive_x.dat'
>>> y = N.loadtxt("archive_x.dat") # Relecture à partir du fichier 'archive_x.dat'
>>> (x == y).all() # Test d'égalité stricte
True
Attention
numpy.loadtxt() supporte les types composés, mais ne
supporte pas les données manquantes; utiliser alors la fonction
numpy.genfromtxt(), plus robuste mais plus lente.
Le format texte n’est pas optimal pour de gros tableaux (ou de rang > 2): il
peut alors être avantageux d’utiliser le format binaire .npy, beaucoup plus
compact (mais non human readable):
>>> x = N.linspace(-1, 1, 1e6)
>>> N.save('archive_x.npy', x) # Sauvegarde dans le fichier 'archive_x.npy'
>>> y = N.load("archive_x.npy") # Relecture à partir du fichier 'archive_x.npy'
>>> (x == y).all()
True
Il est enfin possible de sérialiser les tableaux à l’aide de la bibliothèque standard pickle.
6.1.4. Sous-modules🔗
numpy fournit en outre quelques fonctionnalités
supplémentaires, parmis lesquelles les sous-modules suivants:
numpy.fft: Discrete Fourier Transform;numpy.random: valeurs aléatoires;numpy.polynomial: manipulation des polynômes (racines, polynômes orthogonaux, etc.).
6.1.5. Performances🔗
Avertissement
Premature optimization is the root of all evil – Donald Knuth
Même si numpy apporte un gain significatif en performance par
rapport à du Python standard, il peut être possible d’améliorer la
vitesse d’exécution par l’utilisation de bibliothèques externes dédiées,
p.ex.:
numexpr est un évaluateur optimisé d’expressions numériques:
>>> a = N.arange(1e6) >>> b = N.arange(1e6) >>> %timeit a*b - 4.1*a > 2.5*b 100 loops, best of 3: 11.4 ms per loop >>> %timeit numexpr.evaluate("a*b - 4.1*a > 2.5*b") 100 loops, best of 3: 1.97 ms per loop >>> %timeit N.exp(-a) 10 loops, best of 3: 60.1 ms per loop >>> timeit numexpr.evaluate("exp(-a)") # Multi-threaded 10 loops, best of 3: 19.3 ms per loop
bottleneck est une collection de fonctions accélérées, notamment pour des tableaux contenant des NaN ou pour des statistiques glissantes;
theano, pour optimiser l’évaluation des expressions mathématiques sur les tableaux
numpy, notamment par l’utilisation des GPU et de code C généré à la volée.
Voir également Profilage et optimisation.
6.2. Scipy🔗
scipy est une bibliothèque numérique 1 d’algorithmes et de
fonctions mathématiques, basée sur les tableaux numpy.ndarray,
complétant ou améliorant (en termes de performances) les fonctionnalités de
numpy.
Note
N’oubliez pas de citer scipy & co. dans vos publications et présentations utilisant ces outils.
6.2.1. Tour d’horizon🔗
scipy.special: fonctions spéciales (fonctions de Bessel, erf, gamma, etc.).scipy.integrate: intégration numérique (intégration numérique ou d’équations différentielles).scipy.optimize: méthodes d’optimisation (minimisation, moindres-carrés, zéros d’une fonction, etc.).scipy.interpolate: interpolation (interpolation, splines).scipy.fft: transformées de Fourier.scipy.signal: traitement du signal (convolution, corrélation, filtrage, ondelettes, etc.).scipy.linalg: algèbre linéaire.scipy.stats: statistiques (fonctions et distributions statistiques).scipy.ndimage: traitement d’images multi-dimensionnelles.scipy.io: entrées/sorties.
Liens:
Voir également:
Scikits: modules plus spécifiques étroitement liés à
scipy, parmi lesquels:scikit-learn: machine learning,
scikit-image: image processing,
statsmodel: modèles statistiques (tutorial),
Exercices:
Quadrature et zéro d’une fonction ★, Schéma de Romberg ★★, Méthode de Runge-Kutta ★★
6.2.2. Quelques exemples complets🔗
Interpolation (scipy.interpolate) (interpolation, lissage)
Integration (scipy.integrate) (intégrales numériques, équations différentielles)
Optimization (scipy.optimize) (moindres carrés, ajustements, recherche de zéros)
Signal Processing (scipy.signal) (splines, convolution, filtrage)
Linear Algebra (scipy.linalg) (systèmes linéaires, moindres carrés, décompositions)
Statistics (scipy.stats) (variables aléatoires, distributions, tests)
6.3. Matplotlib🔗
Matplotlib est une bibliothèque graphique de visualisation 2D (avec un support pour la 3D, l’animation et l’interactivité), permettant des sorties de haute qualité « prêtes à publier ». C’est à la fois une bibliothèque de haut niveau, fournissant des fonctions de visualisation « clés en main » (échelle logarithmique, histogramme, courbes de niveau, etc., voir la galerie), et de bas niveau, permettant de modifier tous les éléments graphiques de la figure (titre, axes, couleurs et styles des lignes, etc., voir Anatomie d’une figure).
6.3.1. pylab vs. pyplot🔗
Il existe (schématiquement) deux interfaces pour deux types d’utilisation:
pylab: interface procédurale, originellement très similaire à MATLAB™ et généralement réservée à l’analyse interactive:>>> from pylab import * # DÉCONSEILLÉ DANS UN SCRIPT! >>> x = linspace(-pi, pi, 100) # pylab importe numpy dans l'espace courant >>> plot(x, sin(x), 'b-', label="Sinus") # Trace la courbe y = sin(x) >>> plot(x, cos(x), 'r:', label="Cosinus") # Trace la courbe y = cos(x) >>> xlabel("x [rad]") # Ajoute le nom de l'axe des x >>> ylabel("y") # Ajoute le nom de l'axe des y >>> title("Sinus et Cosinus") # Ajoute le titre de la figure >>> legend() # Ajoute une légende >>> savefig("simple.png") # Enregistre la figure en PNG
matplotlib.pyplot: interface orientée objet, préférable pour les scripts:import numpy as N import matplotlib.pyplot as P x = N.linspace(-N.pi, N.pi, 100) fig, ax = P.subplots() # Création d'une figure contenant un seul système d'axes ax.plot(x, N.sin(x), c='b', ls='-', label="Sinus") # Courbe y = sin(x) ax.plot(x, N.cos(x), c='r', ls=':', label="Cosinus") # Courbe y = cos(x) ax.set_xlabel("x [rad]") # Nom de l'axe des x ax.set_ylabel("y") # Nom de l'axe des y ax.set_title("Sinus et Cosinus") # Titre de la figure ax.legend() # Légende fig.savefig("simple.png") # Sauvegarde en PNG
Dans les deux cas, le résultat est le même:
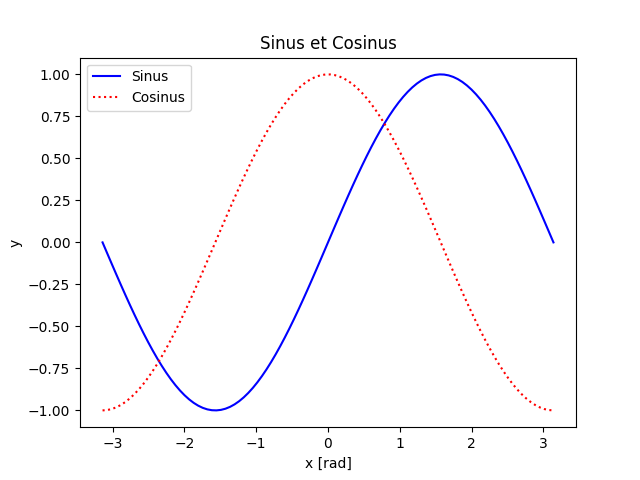
Par la suite, nous nous concentrerons sur l’interface OO matplotlib.pyplot, plus puissante et flexible.
6.3.2. Figure et axes🔗
L’élément de base est le système d’axes matplotlib.axes.Axes, qui
définit et réalise la plupart des éléments graphiques (tracé de courbes,
définition des axes, annotations, etc.). Un ou plusieurs de ces systèmes
d’axes sont regroupés au sein d’une matplotlib.figure.Figure.
La méthode la plus simple pour générer simultanément une figure et un ou
plusieurs systèmes axes est d’utiliser la fonction de haut niveau
matplotlib.pyplot.subplots(), p.ex.:
fig, ax = P.subplots() # génère une figure et un système d'axes
fig, (axG, axD) = P.subplots(nrows=1, ncols=2) # 1 fig, 2 axes en ligne
Ainsi, pour générer une figure contenant 2 (vertical) × 3 (horizontal) = 6 systèmes d’axes (numérotés de 1 à 6):
fig, axs = P.subplots(nrows=2, ncols=3) # 1 fig, liste de 2×3 axes
for (i, j), ax in N.ndenumerate(axs):
ax.set(xticks=[], yticks=[])
ax.text(0.5, 0.5,
f"axs[{i}][{j}]\n#{i*axs.shape[1] + j + 1}",
ha='center', va='center', size='large')
fig.suptitle("fig, axs = P.subplots(nrows=2, ncols=3)", fontsize='x-large')

Pour un contrôle plus fin de la disposition des systèmes d’axes dans une figure,
il est possible de générer les axes un à un via la méthode
matplotlib.figure.Figure.add_subplot():
fig = P.figure()
for i in range(1, 4):
ax = fig.add_subplot(2, 3, i, xticks=[], yticks=[])
ax.text(0.5, 0.5, f"subplot(2, 3, {i})",
ha='center', va='center', size='large')
for i in range(3, 5):
ax = fig.add_subplot(2, 2, i, xticks=[], yticks=[])
ax.text(0.5, 0.5, f"subplot(2, 2, {i})",
ha='center', va='center', size='large')
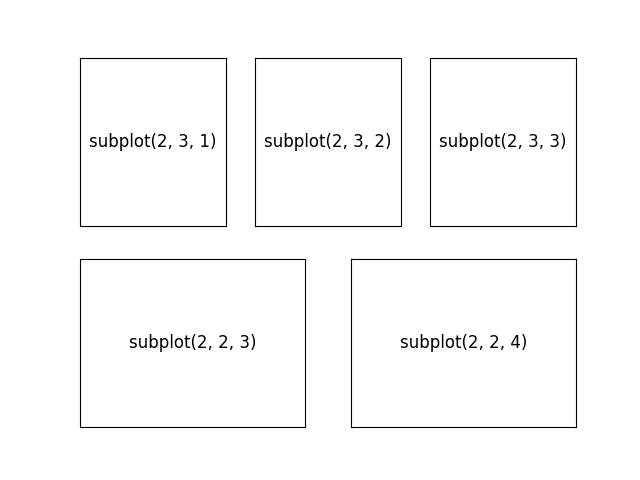
Pour des mises en page plus complexes, il est possible d’utiliser le kit gridspec, p.ex.:
from matplotlib.gridspec import GridSpec
fig = P.figure()
fig.suptitle("grid = GridSpec(2, 3)", fontsize='x-large')
grid = GridSpec(2, 3)
ax1 = fig.add_subplot(grid[0, :-1], xticks=[], yticks=[])
ax1.text(0.5, 0.5, "grid[0, :-1]", ha='center', va='center', size='large')
ax2 = fig.add_subplot(grid[:, -1], xticks=[], yticks=[])
ax3.text(0.5, 0.5, "grid[:, -1]", ha='center', va='center', size='large')
ax3 = fig.add_subplot(grid[1, 0], xticks=[], yticks=[])
ax3.text(0.5, 0.5, "grid[1, 0]", ha='center', va='center', size='large')
ax4 = fig.add_subplot(grid[1, 1], xticks=[], yticks=[])
ax4.text(0.5, 0.5, "grid[1, 1]", ha='center', va='center', size='large')
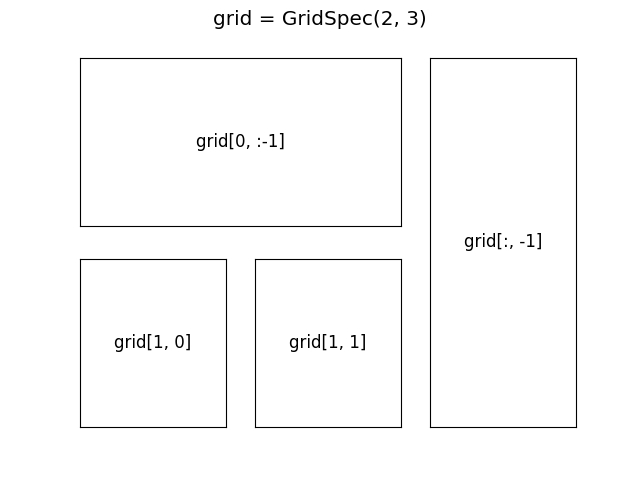
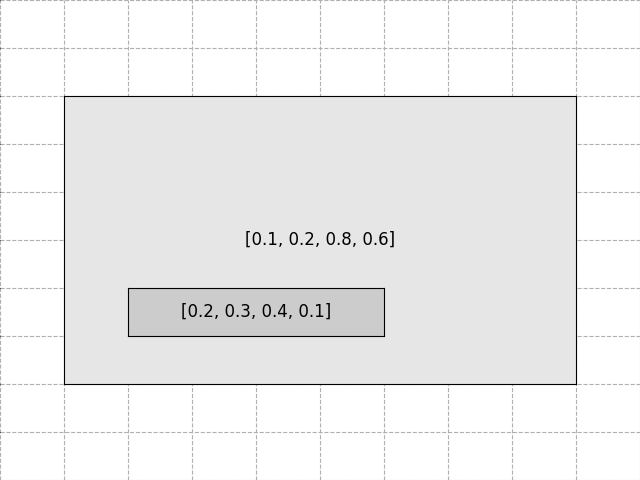
Enfin, il est toujours possible de créer soi-même le système d’axes dans les coordonnées relatives à la figure:
fig = P.figure()
ax0 = fig.add_axes([0, 0, 1, 1], frameon=False,
xticks=N.linspace(0, 1, 11), yticks=N.linspace(0, 1, 11))
ax0.grid(True, ls='--')
ax1 = fig.add_axes([0.1, 0.2, 0.8, 0.6], xticks=[], yticks=[], fc='0.9')
ax1.text(0.5, 0.5, "[0.1, 0.2, 0.8, 0.6]", ha='center', va='center', size='large')
ax2 = fig.add_axes([0.2, 0.3, 0.4, 0.1], xticks=[], yticks=[], fc='0.8')
ax2.text(0.5, 0.5, "[0.2, 0.3, 0.4, 0.1]", ha='center', va='center', size='large')
6.3.3. Sauvegarde et affichage interactif🔗
La méthode matplotlib.figure.Figure.savefig() permet de
sauvegarder la figure dans un fichier dont le format est
automatiquement défini par son extension, png (raster), [e]ps,
pdf, svg (vector), etc., via différents backends.
Il est également possible d’afficher la figure dans une fenêtre interactive avec la commande
matplotlib.pyplot.show():

Note
Utiliser ipython --pylab pour l’utilisation intéractive des figures dans une session ipython.
6.3.4. Anatomie d’une figure🔗
L’interface OO matplotlib.pyplot donne accès à
tous les éléments d’une figure (titre, axes, légende, etc.), qui peuvent alors
être ajustés (couleur, police, taille, etc.).

Fig. 6.1 Figure: Anatomie d’une figure.🔗
Note
N’oubliez pas de citer matplotlib dans vos publications et présentations utilisant cet outil.
Liens:
Voir également:
Third party packages, une liste de bibliothèques complétant
matplotlib: cartographie, visualisation interactive, implémentation de la Grammar of Graphics, graphiques spécialisés, animations, interactivité, etc.mpld3, un backend matplotlib interactif basé sur la bibliothèque web 3D.js;
Seaborn, une surcouche de visualisation statistique à matplotlib et Pandas et xarray;
Bokeh, une bibliothèque graphique alternative à matplotlib plus orientée web/temps réel;
plotext, termplotlib, pour réaliser des figures directement dans le terminal (voir également le backend drawilleplot).
Exemples:
Exercices:
Quartet d’Anscombe ★, Ensemble de Julia ★★, Diagramme de bifurcation: la suite logistique ★★
6.3.5. Visualisation 3D🔗
Matplotlib fournit d’emblée une interface mplot3d pour des figures 3D assez simples:

Fig. 6.2 Figure: Exemple de figure matplotlib 3D.🔗
Pour des visualisations plus complexes, mayavi.mlab est une bibliothèque graphique de visualisation 3D s’appuyant sur Mayavi.
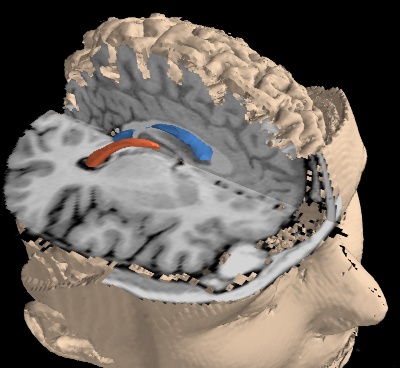
Fig. 6.3 Figure: Imagerie par résonance magnétique.🔗
Note
N’oubliez pas de citer mayavi dans vos publications et présentations utilisant cet outil.
Voir également:
VPython: 3D Programming for Ordinary Mortals;
Glowscript: VPython dans le navigateur;
ipyvolume: visualisation 3D dans le notebook Jupyter.
Notes de bas de page et références bibliographiques
